01 Recall ordinary derivatives If y is a function of x then dy dx is the derivative meaning the gradient (slope of the graph) or the rate of change with respect to x 02 Functions of 2Example Consider the function f(x;y) = 4 1 4 (x 2 y2) To understand the graph of z= f(x;y), we can study trace curves The vertical trace curves are curves made by intersecting the graph with planes of either constant xor y Clearly, if y= kis constant, the equation z= 4 1 4 (x 2 k2) gives a downward opening parabola147 Maxima and minima Suppose a surface given by f ( x, y) has a local maximum at ( x 0, y 0, z 0);

Differentiating Related Functions Intro Video Khan Academy
Partial derivative of 1/sqrt(x^2 y^2 z^2)
Partial derivative of 1/sqrt(x^2 y^2 z^2)-So, let's first differentiate w with respect to x (delw)/(delx) = (del)/(delx)sqrt(x^2 y^2 z^2) (delw)/(delx) = 1/2 * (x^2 y^2 z^2) ^(1/2) * (del)/(delx)(x^2 y^2 z^2) (delw)/(delx) = 1/color(red)(cancel(color(black)(2))) * 1/sqrt(x^2 y^2 z^2) * (color(red)(cancel(color(black)(2)))x 0 0) (delw)/(delx) = color(green)(x/sqrt(x^2 y^2 z^2)) You don't need to calculate the other two partialFind the Indicated partial derivative z=7(y^3)(x^4) 3(y^4)(x^3) ;




Partial Derivatives Calculus 3
I am facing some problem about derivatives in spherical coordinates in spherical coordinates x=r sinθ cos\\phi y=r sinθ sin\\phi z=r cosθ and r=\\sqrt{x^{2}y^{2מחשבונים לאלגברה, חשבון אינפיטיסימלי, גאומטריה, סטטיסטיקה, וכימיה כולל הדרךDraw graph Edit expression Direct link to this page Value at x= Derivative Calculator computes derivatives of a function with respect to given variable using analytical differentiation and displays a stepbystep solution It allows to draw graphs of
And now we want to find the first derivative under function which match in the Z And then here we know that is there will be the variable x quite a bit of constant So the derivative First we need a blind that the review What is the square root for?Directional Derivative Formula Let f be a curve whose tangent vector at some chosen point is v The directional derivative calculator find a function f for p may be denoted by any of the following So, directional derivative of the scalar function is f (x) = f (x_1, x_2, , x_ {n1}, x_n) with the vector v = (v_1, v_2, , v_n) is theWe have, as you write correctly, $$ \def\p#1#2#3{\frac{\partial^{#3} #2}{\partial #1^{#3}}}\p x{}{} f(r) = f'(r)\p x r{} $$ Taking another derivative, we have, using
Answer (1 of 2) The context appears to be classical (Lagrangian) mechanics The overdot is just shorthand for differentiation with respect to time That is, \dot{x}\equiv dx/dt, for instance More importantly, what you are differentiating is the action In Lagrangian physics, the action is treCalculadoras gratuitas paso por paso para álgebra, Trigonometría y cálculoVerify that the function U = (x^2 y^2 z^2)^ (1/2) is a solution of the threedimensional Laplace equation Uxx Uyy Uzz = 0 First I solved for the partial derivative Uxx, Ux = 2x (1/2) (x^2 y^2 z^2)^ (3/2) = x (x^2 y^2 z^2)^ (3/2) Uxx




Multivariate Functions And Partial Derivatives Sage Research Methods




Solved Find The Value Let F X Y Xy 2 Squareroot X Chegg Com
Zy zy= 21(y^2)(x^4) 12(y^3)(x^3) Find the Indicated partial derivative z= 12e^(x^4) y ;zxxConverting this to a unit vector, we have <2,1>/sqrt(5) Hence, Directions of Greatest Increase and DecreaseGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
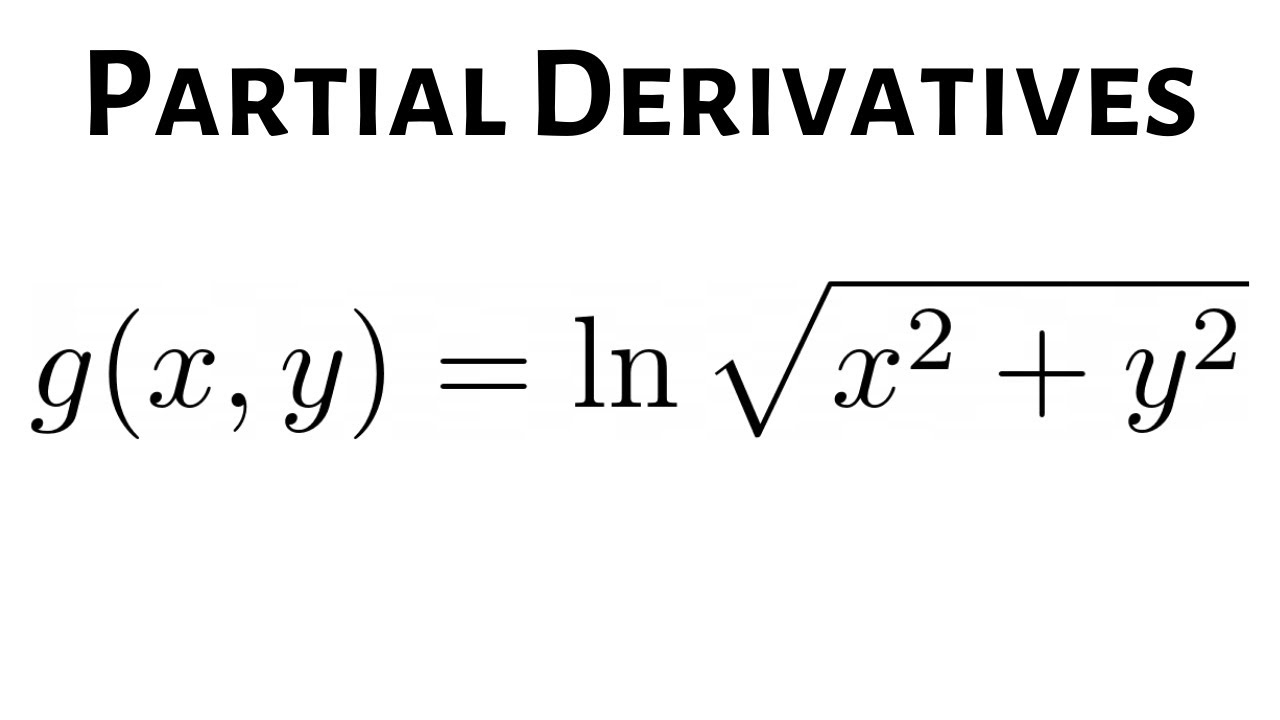



Larson Calculus 13 3 28 First Partial Derivatives Of G X Y Ln Sqrt X 2 Y 2 Youtube



2
Derivative of x/(x^2y^2) by x = (y^2x^2)/(y^42*x^2*y^2x^4) Show a step by step solution;Partially differentiate functions stepbystep \square!Lecture 9 Partial derivatives If f(x,y) is a function of two variables, then ∂ ∂x f(x,y) is defined as the derivative of the function g(x) = f(x,y), where y is considered a constant It is called partial derivative of f with respect to x The partial derivative with respect to y is defined similarly We also use the short hand notation




Trigonometric Substitution Wikipedia
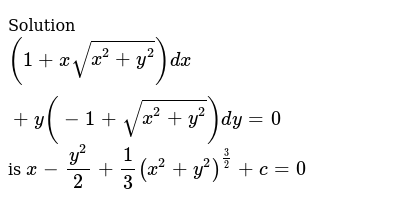



Solution 1 Xsqrt X 2 Y 2 Dx Y 1 Sqrt X 2 Y 2 Dy 0 Is X Y 2 2 1 3 X 2 Y 2 3 2 C 0
Geometrically, this point on the surface looks like the top of a hill If we look at the crosssection in the plane y = y 0, we will see a local maximum on the curve at ( x 0, z 0), and we know from singlevariable calculus that ∂ z ∂ x = 0At the point x=1 and y=1 The direction u is <2,1>Human function have x y z e cocina squared off no size square X plus Sigh square Why plus size square See?




If U F R Where R 2 X 2 Y 2 Then 2u X 2 2u Y 2



Blog Page 119 Of 173 Stumbling Robot
Here we have used the chain rule and the derivatives d d t ( u 1 t x 0) = u 1 and d d t ( u 2 t y 0) = u 2 The vector f x, f y is very useful, so it has its own symbol, ∇ f, pronounced del f'';Includes with respect to x, y and zFree Multivariable Calculus calculator calculate multivariable limits, integrals, gradients and much more stepbystep




If Sqrt 1 X 2 Sqrt 1 Y 2 A X Y Show That Dy Dx Sqrt 1 Y 2 1 X 2 Mathematics And Statistics Shaalaa Com




Second Derivatives Implicit Equations Find Expression Video Khan Academy



0 件のコメント:
コメントを投稿